投稿时间：2007-05-20 21:37:36 jyy630907@163.com

 

　　本人已发表了《关于“四色问题”的证明》和《彻底解决“四色问题”》两篇文章，用的是在最大平面（即球面）上一点一点增加点及连线的方法，证明无论点和线如何增加，都是形成三点包围一点的图形，从而得出最大平面图上“四色足够”的结论。用增加法分析最大平面图，当落在两点连线中的点增多时，就会使整个平面图变得越来越复杂，增加的点难以分辨出是落在哪个三棱锥的一条棱上。再说要我们分析的最大平面图是已经星罗棋布的摆满各个点，并蛛网似的连上了各条线，要在这么复杂的图中分析出无数个一环套一环的三点包围一点图形确实很困难。

　　不过本人经过仔细分析研究，可用一个非常简单的减少法把复杂的最大平面图一步步变成简单。所谓减少法就是把任何一个周围许多点包围中间一点的图形的中间点去掉，并且使周围的多边形在不改变与外界关系的前提下转化成线段和三角形。

　　我们先来看一条公路状的平面图的着色（如图1所示），公路起点用一整块红色，左右车道向下对称的分别用绿、红、绿、红……一块块涂色。当起点终点及左右两边总块数加起来是偶数2n时，终点也是一整块并且n是偶数也用红色，n是奇数用绿色（图1a）。当起点终点及左右两边总块数加起来是奇数2n+1时，终点左右分两块，其中一块沿用上面车道着色方法用红或绿，另一块就要多用一种颜色蓝（图1b）。中间用黄色把左右车道分隔开来，这样图1a就需要三种颜色，图1b就需要四种颜色。因为中间的黄色是被包围在公路当中不与外界接触，它的存在与否不会影响公路外地域的着色情况，所以可以把黄色部分去掉，去掉中间部分后左右车道就合二为一（如图2所示），图2中a和b两种情况与外界的着色关系与图1中a和b两种情况与外界的关系仍旧一样。

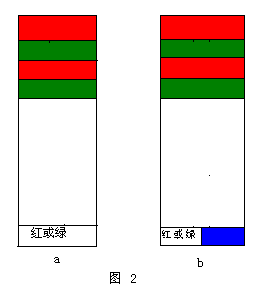
　　我们把上述块状图也画成点与线的关系图的话，图1a和b就分别成了2n个点包围一个点和2n+1个点包围一个点的图。而图2a和b就成了图3a和b的图，即a成了n条线段把n+1个点从起点到终点串联起来；b也成了n条线段把n+1个点从起点到终点串联起来，再在最后两个点的旁边多出一个点。这样的图在减去中间点同时通过左右对称点的合并，共计比原图减少了n个点、2n个面、3n条线。在最大平面图上可以把任何一个点当作中间点来减去，在操作时最好先去掉周围点少的，这样任何复杂的最大平面图到最后只剩下三角形或者三点包围一点的图形。